Can you come up with other, better, divisions?
source.
180 Days of Ideas for Discussion in Math Class. (as of 9July2014, we're in overtime!)
Thursday, December 17, 2015
Wednesday, December 16, 2015
512: Factory Ratios 3
We started with this:
If the ugly-sweater party was held in that factory with the minimum number of workers possible and the ratio of red to green ugly sweaters was 7:13, how likely is it that a left-handed man wore a red ugly sweater?
Source:
In a factory, the ratio of men to women is 2:3. The ratio of right-handed men to left-handed men is 7:3. The ratio of right-handed women to left-handed women is 11:1. What fraction of the factory workforce is right-handed?
And then we extended with: What is the fewest number of employees possible in this building?
And then we extended with: What is the fewest number of employees possible in this building?
If the ugly-sweater party was held in that factory with the minimum number of workers possible and the ratio of red to green ugly sweaters was 7:13, how likely is it that a left-handed man wore a red ugly sweater?
Source:
New GCSE Maths question:
Ratio and proportion is the buzz thing!
How are your students going to tackle it? pic.twitter.com/RyPsmc9z4m
— m4ths.com (@m4thsdotcom) December 16, 2015
511: Factory Ratios 2
We started with this:
What is the fewest number of employees possible in this building?
Source:
In a factory, the ratio of men to women is 2:3.
The ratio of right-handed men to left-handed men is 7:3
The ratio of right-handed women to left-handed women is 11:1
What fraction of the factory workforce is right-handed?
But let's extend things a bit.The ratio of right-handed men to left-handed men is 7:3
The ratio of right-handed women to left-handed women is 11:1
What fraction of the factory workforce is right-handed?
What is the fewest number of employees possible in this building?
Source:
New GCSE Maths question:
Ratio and proportion is the buzz thing!
How are your students going to tackle it? pic.twitter.com/RyPsmc9z4m
— m4ths.com (@m4thsdotcom) December 16, 2015
510: Factory Ratios 1
In a factory, the ratio of men to women is 2:3.
The ratio of right-handed men to left-handed men is 7:3
The ratio of right-handed women to left-handed women is 11:1
What fraction of the factory workforce is right-handed?
Source:
The ratio of right-handed men to left-handed men is 7:3
The ratio of right-handed women to left-handed women is 11:1
What fraction of the factory workforce is right-handed?
Source:
New GCSE Maths question:
Ratio and proportion is the buzz thing!
How are your students going to tackle it? pic.twitter.com/RyPsmc9z4m
— m4ths.com (@m4thsdotcom) December 16, 2015
Saturday, November 28, 2015
509: Circles 2
Several days ago, I posted a slightly different question about tangential circles and the spaces in between. Compare this question, from the 2004 SAT Practice Test to that question from Emma Bell.
source: ETS, 2004
- Which question seems harder? What are the difficult aspects of each?
- Do we have to specify the angle APB?
- How are these two questions different in terms of the knowledge they require for solving?
- Is this question made harder by the "how many times" part? Does that phrasing make the question unnatural?
source: ETS, 2004
Sunday, November 22, 2015
507: Orderly Probability
Scenario 1: Which winning number group is more likely to occur?
Scenario 2: Which winning number group is more likely to occur if the numbers are drawn in any order and THEN put into ascending order by the presenter?
In which of the above two scenarios is getting the winning numbers more likely?
source: Jeff Suzuki
1-2-3-4-5-6 OR 4-8-15-16-23-42
Scenario 2: Which winning number group is more likely to occur if the numbers are drawn in any order and THEN put into ascending order by the presenter?
1-2-3-4-5-6 OR 4-8-15-16-23-42
In which of the above two scenarios is getting the winning numbers more likely?
source: Jeff Suzuki
506: The Conical Tank
The last of the three related-rate geogebra problems from Kate Nowak. It's the related rate problem from calculus: the conical tank being filled with water.
Adjust the slider and... wait, what is changing and how?
For every click of the slider:
Is the depth increasing at a constant rate?
Is the radius increasing at a constant rate?
Is the volume increasing at a constant rate?
How can you tell?
If you want to play with the animation, Conical Tank Problem. source: @k8nowak
Adjust the slider and... wait, what is changing and how?
For every click of the slider:
Is the depth increasing at a constant rate?
Is the radius increasing at a constant rate?
Is the volume increasing at a constant rate?
How can you tell?
- Where or how, in the RealWorldtm, could we see the constant increase in volume?
- Where or how, in the RealWorldtm, could we see the constant increase in radius, or depth?
If you want to play with the animation, Conical Tank Problem. source: @k8nowak
505: The Balloon Problem
We've all seen this problem, but many of our students haven't. It's the related rate problem from calculus: the balloon being filled with air.
There are two questions being demonstrated here.
(1) "If the volume increases at a constant rate, what is happening to the radius?" and
(2) "If the radius increases at a constant rate, what is happening to the volume?"
The first question is to figure out which situation is modeled in red and which in blue.
Then we can ask:
If you want to play with the animation, Balloon Problem. source: @k8nowak
There are two questions being demonstrated here.
(1) "If the volume increases at a constant rate, what is happening to the radius?" and
(2) "If the radius increases at a constant rate, what is happening to the volume?"
The first question is to figure out which situation is modeled in red and which in blue.
Then we can ask:
- Does the radius increase at a constant speed in both models? How can you tell?
- Does the volume increase at a constant speed in both models? How can you tell?
- Where or how, in the RealWorldtm, could we see the constant increase in volume?
- Where or how, in the RealWorldtm, could we see the constant increase in radius?
If you want to play with the animation, Balloon Problem. source: @k8nowak
Friday, November 6, 2015
504: The Ladder Problem
We've all seen this problem, but many of our students haven't.
It's the related rate problem from calculus: the ladder sliding down the wall.
The "official" question?
How fast is the ladder's top sliding down the wall if the bottom is being pulled out at a rate of 1 ft/sec?
We can ask a few questions of kids at any level, though, based on the given that the bottom of the ladder is being pulled to the left at 1 foot per sec.
- Does the top drop at a constant speed?
- Does the top drop a distance equal to the horizontal movement?
- When is the speed of the top greater than 1, less than 1, and equal to 1?
- If this is a 25 foot ladder, with the bottom 7 feet out from the base of the wall, and the top drops 4 feet ... how far out does the bottom of the ladder have to go?
If you want to play with the animation, Ladder Problem. source: @k8nowak
Sunday, November 1, 2015
503: Circles
This is a straightforward question. I'd like to make all of you students into teachers for a minute ... Let's create a test question !
- Do we have to specify angle AOB?
- Is there a better way to say something without actually saying it?
- What other instructions and given information could we provide that would lead to the same answer?
- What is the best question here?
502: Powerful Question
It's not included in the PEMDAS Order of Operations ...
Should $a^{b^c} = ({a^b})^c$ or should it be $a^{b^c} = a^{(b^c)}$ ??
Does $3^{2^0}$ equal 1 or 3?
Let's just consider easy numbers {1, 2, 3, 4} so we can explore. What's the probability that the two methods arrive at the same answer?
For the record, $a^{b^c} = a^{(b^c)}$ is the accepted order of operations here.
Should $a^{b^c} = ({a^b})^c$ or should it be $a^{b^c} = a^{(b^c)}$ ??
Does $3^{2^0}$ equal 1 or 3?
Let's just consider easy numbers {1, 2, 3, 4} so we can explore. What's the probability that the two methods arrive at the same answer?
For the record, $a^{b^c} = a^{(b^c)}$ is the accepted order of operations here.
Saturday, October 24, 2015
501: Learning time
Read this post on lost learning time.
Here's his basic point:
Here's his basic point:
In a typical school year, 8,700 minutes not utilized for learning.... roughly 10 of 60 minutes are not spent learning.
In one day, roughly 50 minutes.
In a 5 day week, 250 minutes.
Now, let's be realistic and cut that number in half because we all know there are assemblies and other events that cut into learning time throughout the school year. That leaves us with 4,350 minutes of time not spent learning.
- Do you agree with his analysis?
- How about his calculations?
- What should be done?
Monday, October 19, 2015
500: Secret Salary
My employer has nine workers. The nine of us want to determine what
our average salary is, but none of us wants to divulge his own salary.
Can we find the average without doing so?
source.
source.
499: Blue-Eyed Blondes
If the proportion of blonds among blue-eyed people is greater than among
the population as a whole, is it also true that the proportion of
blue-eyed people among blonds is greater than among the population as a
whole?
source.
source.
498: Circles on a Lattice
On a square lattice, a circle can pass through 2, 3, or 4 points, as in the diagram below. The original question asks for a circle that passes through 5 points, but can you define a circle that passes through other numbers of points? and explain how the circle was created?
source:
source:
On a square lattice, a circle can pass through exactly 2, 3, or 4 points. What about 5? #math #mathchat #MTBoS pic.twitter.com/CsMd6zzbLo
— Matt Enlow (@CmonMattTHINK) August 5, 2015
Sunday, October 11, 2015
495: Pythagorean anti-Triples?
Ask your class if there are any Pythagorean anti-Triples: $\dfrac{1}{a^2} + \dfrac{1}{b^2} = \dfrac{1}{c^2}$ ?
If a, b, c are integers, the question seems harder, since 1/3, 1/4, 1/5 would be (to me) obvious answers - leading to the rules for Pythagorean triples and just using their reciprocals.
Source:
Are there any Pythagorean anti-triples: 1/(a^2) + 1/(b^2) = 1/(c^2) ?
— James Tanton (@jamestanton) October 11, 2015
Saturday, October 10, 2015
494: NetFlix Optimization
An article about the Netflix price hike:
Netflix upped the rate of its “two-screen” plan from $8.99 to $9.99. This plan lets you watch two HD (or regular) streams simultaneously on different devices. Netflix’s “one-screen” and “four-screen” plans remained unaffected.
Here's the thinking: If Netflix subscribers start dropping from the two-screen plans to one-screen plans, this will make them a lot less likely to share their password. No one wants a little offhand altruism to actually affect their viewing habits. That would be bad. If the resulting lack of password-sharers pushes more people to subscribe, then its worth the dollar per subscriber Netflix loses when a user downgrades because of the price increase.
Find the NetFlix subscription numbers to see how the price hike changed things. Was this a good move?
Tuesday, September 29, 2015
493: It Sure Would Be Easier
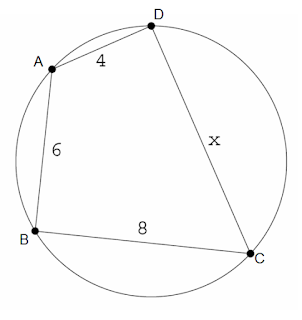
If we are told that we have a quadrilateral inscribed in a circle with diameter 10, do we KNOW if the angle at B and the angle at D are 90°? Because that sure would make it easier to find x.
Sunday, September 27, 2015
Sunday, September 13, 2015
491: Discuss the Errors, part 2
This question is from the NY Regents test, and discussed by Patrick Honner in his long-running series, "Are These Tests Any Good?".
Can your students find what is wrong with it?
How would they fix it?
source.
Can your students find what is wrong with it?
How would they fix it?
source.
490: Discuss the Errors, part 1
These questions are from the NY Regents test, and discussed by Patrick Honner in his long-running series, "Are These Tests Any Good?".
Can your students find what is wrong with them?
and
source.
Can your students find what is wrong with them?
and
source.
Saturday, August 22, 2015
489: Which Quadratic Formula?
So ... I've seen a couple of YouTube videos that feature songs about the Quadratic Formula. I often see it written like this:
and it occurs to me that I've always written it this way:
Which one is better?
$x = \dfrac{-b \pm \sqrt{b^2-4ac}}{2a}$
and it occurs to me that I've always written it this way:
$x = \dfrac{-b}{2a} \pm \dfrac{\sqrt{b^2-4ac}}{2a}$
Which one is better?
Thursday, July 16, 2015
487: The Fifteen Puzzle
Everyone older than ten knows that there is a way to play tic-tac-toe so that you can never lose. Any game that can be played to a draw unless someone makes a newbie's mistake, is boring once you know the secret.
Let's look at this one and see if you can find a strategy for it:
Players alternate writing a number from 1 - 9 (once used, it’s dead). First one with a set of three numbers that sum to 15 wins.
Is there a guaranteed winning strategy for Player 1?
Is there a guaranteed winning strategy for Player 2?
source:
Let's look at this one and see if you can find a strategy for it:
Players alternate writing a number from 1 - 9 (once used, it’s dead). First one with a set of three numbers that sum to 15 wins.
Is there a guaranteed winning strategy for Player 1?
Is there a guaranteed winning strategy for Player 2?
source:
Players alternate writing a number from 1 - 9 (once used, it’s dead). First one with a set of three numbers that sum to 15 wins.
— Chris Lusto (@Lustomatical) July 16, 2015
How does his later comment help? "It’s equivalent to tic-tac-toe since any row/col/diagonal in a 3x3 magic square sums to 15, but more mathematically interesting."
486: The Bowling Pins Puzzle
Everyone older than ten knows that there is a way to play tic-tac-toe so
that you can never lose. Any game that can be played to a draw unless
someone makes a newbie's mistake, is boring once you know the secret.
Let's look at this one and see if you can find a strategy for it:
There are thirteen pins and the two players take turns bowling.When bowling, you can knock down any pin or two adjacent pins (but not two that are separated by a space) that you like. The loser knocks over the last pin.
The gnome has bowled first, knocking down #2. How do you best play this game so that you are guaranteed to win?
If you go first, what is your best play?
source: Loyd's Encyclopedia, 1914.
Let's look at this one and see if you can find a strategy for it:
There are thirteen pins and the two players take turns bowling.When bowling, you can knock down any pin or two adjacent pins (but not two that are separated by a space) that you like. The loser knocks over the last pin.
The gnome has bowled first, knocking down #2. How do you best play this game so that you are guaranteed to win?
If you go first, what is your best play?
source: Loyd's Encyclopedia, 1914.
Monday, July 13, 2015
484: Tempus Fugit
If the time is 10:10, what is the exact angle between the minute hand and hour hand?
How about 7:30?
How about 7:35?
483: Time and Time Again
How many times per day do the hands make a straight angle? What are some of these times?
How many times per day do the hands make a right angle? What are some of these times?
482: Angling for More Time
If the MINUTE hand is on 2, and the hour hand and minute hand make an acute angle, what time could it be?
If the MINUTE hand is on 8, and the hour hand and minute hand make an obtuse angle, what time could it be?
source.
If the MINUTE hand is on 8, and the hour hand and minute hand make an obtuse angle, what time could it be?
source.
Saturday, July 11, 2015
481: Two Circles and One Square
 |
| What is the red area? |
Here is the real question: Does it matter if the circles are congruent, as long as they're tangent and the centers are at the vertices of the square?
A Saturday #Geometry Delight
#SATPrep #mathchat @intmath @JustinAion @Fouss @PDCorner @MathCurmudgeon @bowenkerins pic.twitter.com/V6zcjOfrqW
— David Marain (@dmarain) July 11, 2015
Wednesday, July 8, 2015
Sunday, June 7, 2015
479: Dihedral Angle
What's the angle between the red lines? pic.twitter.com/IXK5GfvM0N
— Will Feavyour (@NextLevelMaths) April 3, 2015
Saturday, June 6, 2015
478: Salinon Areas
source:
The Salinon was first introduced in the Book of Lemmas, a work attributed to Archimedes. http://t.co/crVrwtxeb8
— Cliff Pickover (@pickover) June 6, 2015Thursday, June 4, 2015
Tuesday, June 2, 2015
476: Squares and Cubes
How is this problem
related to this one from a few days back?
related to this one from a few days back?
 |
| Is any square number times four another square number? |
Sunday, May 31, 2015
475: Circle Theorems
Here are eight circle theorems, written by a Brit so you'll have to "translate" to American English ...
Are these the most important ones?
Are there any that are missing that you feel should be included in this group?
source:
Are these the most important ones?
Are there any that are missing that you feel should be included in this group?
source:
Circle Theorems - these are very important to learn for the Higher Tier pic.twitter.com/rG4KOwwixP
— Corbettmaths (@Corbettmaths) May 31, 2015
Friday, May 29, 2015
473: Overlapping Squares
I might have posted this puzzle before.
What do your students think? Can they generalize it?
What is the overlapped area?
source:
What do your students think? Can they generalize it?
What is the overlapped area?
source:
As the red square is rotated around point O, what is the area of the overlap with the yellow square? #geomchat
— David Wees (@davidwees)
Sunday, May 24, 2015
472: How Many geometry Theorems Are There?
That's pretty much it: How many Geometry Theorems are needed to solve this extended problem?
source:
source:
Old Exam Questions #2 : My solution in a few days...
http://t.co/VDHpuoDY5a pic.twitter.com/OFpD7AT6G4
— solve my maths (@solvemymaths) May 24, 2015
471: Digits in Fibonacci
We all recognize the Fibonacci Sequence: 1, 1, 2, 3, 5, 8, 13, 21, ...
What is the units digit of the sixty-first Fibonacci number?
Is there a pattern?
What is the units digit of the sixty-first Fibonacci number?
Is there a pattern?
1,1,2,3,5,8,13,21,... What is the final digit of the sixty-first Fibonacci number?
— James Tanton (@jamestanton) May 24, 2015
470: Poor Alex Bellos
Normally, I'm glad when the nedia talks about math, even if it is simply the latest "Super-Hard problem from Asia that All of Us Stupid American Adults and Brits Won't be Able to Solve but Their 8 Year-old Do Routinely."
Throw in "I gave it to a mathematician and he couldn't solve it either" and you've got an instant viral hit, apparently.
All right, rant over.
What's the error?
Oh, and solve it if you want, too. It's not really that hard.
Further questions:
source.
(answer linked from there)
Throw in "I gave it to a mathematician and he couldn't solve it either" and you've got an instant viral hit, apparently.
All right, rant over.
What's the error?
Oh, and solve it if you want, too. It's not really that hard.
Further questions:
- Which blanks CANNOT have a prime number in them?
- Which blanks COULD have certain prime numbers?
- Which blanks essentially force this problem to be non-unique?
source.
(answer linked from there)
469: Fix this Graph #ILostCount
This graph needs a lot of work.
What information is being presented?
What is the best way to display this information?
Does this graph rely too much on the reader's knowledge of the city?
source.
Tuesday, May 19, 2015
468: Fields of Green
What is the area of the whole hexagonal shape?
Can your students generalize this result?
Source:
Farmer has 3 square fields & 4 triangular fields. What is the entire area of his estate? http://t.co/R8IyU2iyYF pic.twitter.com/3yEdcBrw3N
— Cliff Pickover (@pickover) May 19, 2015
Monday, May 18, 2015
467: Squares
Take a square number and multiply by four. Is it guaranteed to still be a square number?
Can we generalize this rule?
Can your students explain why?
Source:
Can we generalize this rule?
Can your students explain why?
Source:
Subitizing Series #5:
These Dots Will Grow on You
http://t.co/MWtwbjb9eG
Is every sq. # ×4 another square # #mtbos pic.twitter.com/IxwBXCaOGS
— Steve Wyborney (@SteveWyborney) May 18, 2015
Sunday, May 17, 2015
465: Probability Machine
You've all seen Plinko and its variations. Here's one:
This one has a normal curve drawn on the background. Should it be a normal curve or more triangular like the arrangement of the pins?
Would it still be in this shape if the pins were arranged in a rectangle?
This one has a normal curve drawn on the background. Should it be a normal curve or more triangular like the arrangement of the pins?
Would it still be in this shape if the pins were arranged in a rectangle?
463: Illusions 3 - Cafe Wall
Here's the original Cafe Wall, after which the Cafe Wall Illusion was named.
What went wrong with this wall? What is it that every single bricklayer and tile-setter knows as Rule #1, to avoid the Cafe Wall Illusion?
What went wrong with this wall? What is it that every single bricklayer and tile-setter knows as Rule #1, to avoid the Cafe Wall Illusion?
462: Illusions 2
How did this artist lay out the guidelines on this flat, concrete floor for this seemingly 3D artwork?
460: Illusions 1
What is the best way to show that the horizontal lines are, in fact, horizontal and parallel?
Why does your brain insist that they are not?
Why does your brain insist that they are not?
Thursday, May 14, 2015
459: Cubes
Sure, you can ask, "How many?"
But wouldn't you rather see if your students can figure out what kind of fruit is each cube?
Wednesday, May 13, 2015
458: Is That You, Pythagoras?
If we stipulate that $(x+12)^2+(y+4)^2+(z+3)^2=0$, then
$\sqrt{x^2+y^2+z^2}=?$
Should we brute-force this or is there a more beautiful or subtle way of getting what we want?
Source:
$\sqrt{x^2+y^2+z^2}=?$
Should we brute-force this or is there a more beautiful or subtle way of getting what we want?
Source:
(x+12)²+(y+4)²+(z+3)²=0
√(x²+y²+z²)=?
#SATPrep #mathchat #algebra
— David Marain (@dmarain) May 13, 2015
Sunday, May 10, 2015
457: Codebreaker
What are the values of the letters that will allow you to go as far as possible?
How high can you go?
Is there a better way to solve this than just marching up the line, and guessing at the values for H, R, then for F, U, then for I, V and so on?
The original is below. Is this the best set of values?
source:
Negative numbers code-breaker activity with a twist!
#mathschat #MathsTLP pic.twitter.com/bOrXtB7mzS
— MathedUp! (@MathedUp) May 10, 2015
Subscribe to:
Posts (Atom)