180 Days of Ideas for Discussion in Math Class. (as of 9July2014, we're in overtime!)
Sunday, August 31, 2014
235: Counterfeit Bill
The Counterfeit Bill problem (Sobel and Maletsky 1999).
A customer enters a store and purchases a pair of slippers for $5, paying for the purchase with a $20 bill. The merchant, unable to make change, asks the grocer next door to change the bill. The merchant then gives the customer the slippers and $15 change.
After the customer leaves, the grocer discovers that the $20 bill is counterfeit and demands that the shoe-store owner make good for it. The shoe-store owner does so, and by law is obligated to turn the counterfeit bill over to the FBI.
How much does the shoe-store owner lose in this transaction?
A customer enters a store and purchases a pair of slippers for $5, paying for the purchase with a $20 bill. The merchant, unable to make change, asks the grocer next door to change the bill. The merchant then gives the customer the slippers and $15 change.
After the customer leaves, the grocer discovers that the $20 bill is counterfeit and demands that the shoe-store owner make good for it. The shoe-store owner does so, and by law is obligated to turn the counterfeit bill over to the FBI.
How much does the shoe-store owner lose in this transaction?
Saturday, August 30, 2014
234: Fraction Manipulation
I know how I would solve this problem, but not everyone is comfortable with algebra. Which ways can you come up with? Which seems the best to you?
There is a number such that, when it is subtracted from the numerator of the fraction $\dfrac{5323}{7577}$ and added to the denominator, the fraction reduces to $\dfrac{17}{83}$. Determine the number.
There is a number such that, when it is subtracted from the numerator of the fraction $\dfrac{5323}{7577}$ and added to the denominator, the fraction reduces to $\dfrac{17}{83}$. Determine the number.
Friday, August 29, 2014
233: Vegetable Zen
100 students were surveyed about their preferences for bell peppers (capsicum), carrots and spinach, with the following results:
① 72 students said they like bell peppers, and 36 students said they like only bell peppers.
② 41 students said they like carrots, and 9 students said they like only carrots.
③ 31 students said they like spinach, and 3 students said they like only spinach.
④ 9 students said they like neither bell peppers, nor carrots, nor spinach.
What is the best way to model/analyze this survey data?
Graphically (and what type of graph)?
Tables? How?
Algebra?
source.
Thursday, August 28, 2014
Wednesday, August 27, 2014
231: Friedman Numbers
How do you suppose we could go about finding these?
Any methods or algorithms that we might use?
Source.
Challenge: How would we determine whether this is an infinite set or a finite one?
Any methods or algorithms that we might use?
Source.
Challenge: How would we determine whether this is an infinite set or a finite one?
Tuesday, August 26, 2014
229: Create a special 10-digit number
Can you create a 10-digit number, where the first digit is how many
zeros in the number, the second digit is how many 1s in the number etc.
until the tenth digit which is how many 9s in the number?
Some hints:
Can it be 0000000000?
Can it be 9000000000?
Source: Richard Wiseman.
One answer, slightly obfuscated, is 2³ * 5³ * 7 * 887143
Some hints:
Can it be 0000000000?
Can it be 9000000000?
Source: Richard Wiseman.
One answer, slightly obfuscated, is 2³ * 5³ * 7 * 887143
Monday, August 25, 2014
228: Four Intersections
Find two polynomials whose four points of intersection form a perfect square. (...with integer coefficients?)
What's the best way to do that?
.
What's the best way to do that?
Find two polynomials whose four points of intersection form a perfect square.
(...with integer coefficients?)
— James Tanton (@jamestanton) July 5, 2014
@jamestanton 13*x^3/15+13*x^2/10-137*x/30 & x^4+43*x^3/15-37*x^2/10-317*x/30 go through square with vertices (0,0), (2,3), (-1,5), (-3,2)
— Republic of Math (@republicofmath) July 5, 2014
. .
Saturday, August 23, 2014
227: Are these the Same?
Are these the same or not the same? Why? (What makes them different if you think they're different?)
source.
source.
Friday, August 22, 2014
225: Penny circle
Here's a screen grab of one of @ddmeyer's videos: Penny Circle.
If this were a 0.75" circle, the penny would fit perfectly. If it's 1" then there would be a lot of wasted space. What sizes of circle would be best for packing in 0.75" pennies with as little wasted space as possible?
If this were a 0.75" circle, the penny would fit perfectly. If it's 1" then there would be a lot of wasted space. What sizes of circle would be best for packing in 0.75" pennies with as little wasted space as possible?
Thursday, August 21, 2014
Wednesday, August 20, 2014
223: Combination (?) Locks 1
Which one is most secure?
Three numbers ...
This one with three extra wheels you can swap in ...
Or this one, with three letters?
Three numbers ...
This one with three extra wheels you can swap in ...
Or this one, with three letters?
Tuesday, August 19, 2014
222: Which would you rather push?
Would you rather ...
Which one is "easier"?
Which one is "easier"?
Would You Rather...? with a physics twist.
— John Stevens (@Jstevens009)
Monday, August 18, 2014
Sunday, August 17, 2014
220: Three Scales
There are three scales.
The one on the right (navy shirt) indicates a 10 N force to the right ... +10 N.
The one on the left (green shirt) indicates a 10 N force to the left ... -10 N.
What will the scale in the middle read?
Thanks to @fnoschese for posting this.
The one on the right (navy shirt) indicates a 10 N force to the right ... +10 N.
The one on the left (green shirt) indicates a 10 N force to the left ... -10 N.
What will the scale in the middle read?
Thanks to @fnoschese for posting this.
Saturday, August 16, 2014
219: How far out can you go?
A series of identical blocks.
A series of identical rectangular blocks is stacked out at their balancing points from the top down. You can show with a simple center of mass calculation the total "stick-out" distance; that is, the horizontal distance from the back of the bottom block to the back of the top block is
d = ½(1 + ½ + ⅓ + ¼ + ...)
Thanks to @fnoschese for finding these.
A series of identical rectangular blocks is stacked out at their balancing points from the top down. You can show with a simple center of mass calculation the total "stick-out" distance; that is, the horizontal distance from the back of the bottom block to the back of the top block is
d = ½(1 + ½ + ⅓ + ¼ + ...)
Thanks to @fnoschese for finding these.
Friday, August 15, 2014
Thursday, August 14, 2014
217: Twelve dots and triangles
Here are twelve dots equally spaced around a circle. There are two triangles created by connecting three of the dots.
Challenge:
What are those two areas?
Source: https://solvemymaths.wordpress.com/
- Which three dots will give the triangle with the LARGEST area?
- Which three dots will give the triangle with the SMALLEST area?
Challenge:
What are those two areas?
Source: https://solvemymaths.wordpress.com/
Wednesday, August 13, 2014
216: Circles in a Rectangle
This one is going to need a whole-class, team effort.
.
.
Last brain buster before end of term. Tough one. Can you solve it? https://t.co/fj90odpFie #mathchat #mathschat pic.twitter.com/aDWSTmGP2Z
— Ed Southall (@edsouthall) July 13, 2014
Source: https://solvemymaths.wordpress.com/
Tuesday, August 12, 2014
215: Units Digit Redux
What's the best way to go about figuring this one out? Is it like the previous one?
Source:
.@MATHCOUNTS Math Challenge Problem #mathchat pic.twitter.com/071Kvg8smg
— MathMovesU (@mathmovesu) July 10, 2014
Monday, August 11, 2014
214: Last Digit
What is the last digit (units digit) in the expansion of 39999?
How can we find this digit with tech?
Without tech?
Which way is more "clever"?
Which way gives you more satisfaction?
How can we find this digit with tech?
Without tech?
Which way is more "clever"?
Which way gives you more satisfaction?
Sunday, August 10, 2014
Saturday, August 9, 2014
212: Hold on there, Triangle
Take a moment to find the areas of both triangles. Check that the pieces of both triangles are the same shapes and sizes.
What topic in algebra I is a really good way to explain this?
What topic in algebra I is a really good way to explain this?
Friday, August 8, 2014
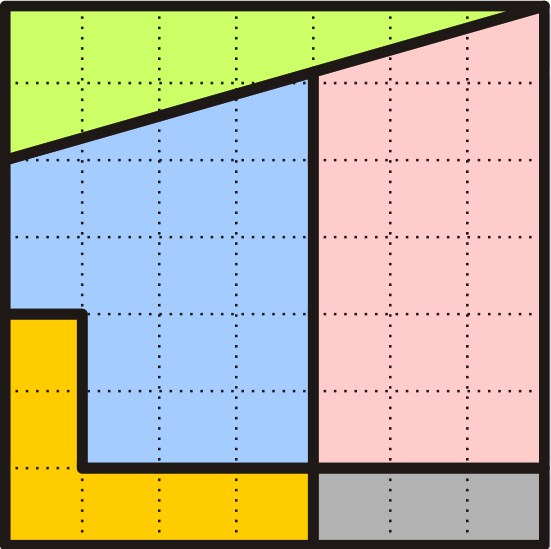
211: Wait a Minute, Square.
Take a moment to check that each piece in the top diagram is identical to its counterpart in the bottom one.
If you want to recreate this in Geogebra ...
If you want to recreate this in Geogebra ...
- turn on grid.
- insert the polygons in this order: green triangle, black rectangle, yellow L-shape.
- insert a segment up the "middle" at the appropriate x-position.
- locate the intersection point of the segment and the hypotenuse of the triangle.
- insert the two final polygons.
- Click on each polygon, and copy-paste and build the second figure below the first one.
Thursday, August 7, 2014
210: Rationally Radical
We all know it's possible to multiply two radicals together and get an integer result.
( √7 ) * ( √7 ) = 7 is one possibility.
Is it possible to ADD two or more radicals and get a rational result?
( √7 ) * ( √7 ) = 7 is one possibility.
Is it possible to ADD two or more radicals and get a rational result?
Wednesday, August 6, 2014
209: Lewis Carrol's Roses
Nine roses are planted in a circle. If you find that tedious, show how you can rearrange the roses to get:
- Eight rows of three-in-a-row.
- Nine rows of three-in-a-row.
- Ten rows of three-in-a-row.
from Lewis Carroll.
Tuesday, August 5, 2014
208: Three Questions
Consider the following diagram from the SAT in which the identical circles are tangent to each other and the vertices of the triangle are the centers of the circles.:
What is an easy question they might ask?
What is a medium difficulty question?
What is a hard question?
What is an easy question they might ask?
What is a medium difficulty question?
What is a hard question?
Monday, August 4, 2014
207: Sequence of a
Consider the sequence: 1, a , a2, a3, ... , an
Is the median of that sequence more than, less than, or equal to an/2 ?
What values of a could make this a dodgy question?
Is the median of that sequence more than, less than, or equal to an/2 ?
What values of a could make this a dodgy question?
Sunday, August 3, 2014
Saturday, August 2, 2014
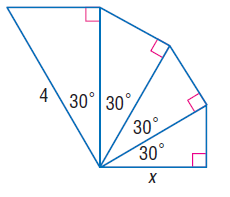
205: Special Triangle Spiral
If the side marked "x" is considered the beginning, and this pattern continued CCW, getting larger infinitely, how many sides would be of integer length?
Friday, August 1, 2014
Subscribe to:
Posts (Atom)