180 Days of Ideas for Discussion in Math Class. (as of 9July2014, we're in overtime!)
Tuesday, September 30, 2014
266: Lending $50
If I were to give you $50 we'd have the same amount. If you were to give me $50 I'd have 9 times as much as you. How much do we each have?
Source.
Sunday, September 28, 2014
265: Nix The Tricks
- Which of the following "tricks" was helpful to you in learning and understanding what was going on?
- Which ones just got you confused when the problem changed form slightly?
- Did you ever confuse $\dfrac{3}{5}x\dfrac{1}{5}$ with $\dfrac{3}{5} = \dfrac{x}{5}$ with $\dfrac{3}{5} + \dfrac{1}{4}$?
Which "tricks" should teachers stop using?
264: Add Operators
Using only the symbols +, -, *, and ÷ as replacement for the blanks, find the greatest value of the expression given.
What would be the greatest value if you could also use parentheses?
How do you know this is the largest value?
source: Algebra Problems, Dale Seymour.
1 ___ 2 ___ 3 ___ 4 ___ 5 ___ 6 ___ 7 ___ 8
What would be the greatest value if you could also use parentheses?
How do you know this is the largest value?
source: Algebra Problems, Dale Seymour.
Saturday, September 27, 2014
263: Make Equal with Parentheses
Insert parentheses into each of the following expressions so that each will have the same value.
Algebra Problems, Dale Seymour.
4 + 3 * 7 - 4
2 * 3 + 3 * 5
2 * 5 - ½ * 10 * 9
3² ÷ ⅓ + 3 * 6
Algebra Problems, Dale Seymour.
Friday, September 26, 2014
Thursday, September 25, 2014
Wednesday, September 24, 2014
Tuesday, September 23, 2014
259: Another Sets Puzzle
There are 40 students in the Travel Club. They discovered that 17 members have visited Mexico, 28 have visited Canada, 10 have been to England, 12 have visited both Mexico and Canada, 3 have been only to England and 4 have been only to Mexico. Some club members have not been to any of the three foreign countries and an equal number have been to all three countries. How many students have been to all three countries?
Source: UVM, 2011
Source: UVM, 2011
Monday, September 22, 2014
258: Roots of an equation.
There's nothing RealWorld about this question.
The two roots of the quadratic equation x² - 85x + c = 0 are prime numbers. What is the value of c?
What part of that sentence is the most important - that couldn't be left out and still have a solution.?
The two roots of the quadratic equation x² - 85x + c = 0 are prime numbers. What is the value of c?
What part of that sentence is the most important - that couldn't be left out and still have a solution.?
Sunday, September 21, 2014
257: Two Triangles
We have this "hard" SAT question:
How could we redraw this to make it simpler to see and understand the solution?
In the figure above, if AB = 4, BC = 24, and AD = 26, then CD = ?
How could we redraw this to make it simpler to see and understand the solution?
Saturday, September 20, 2014
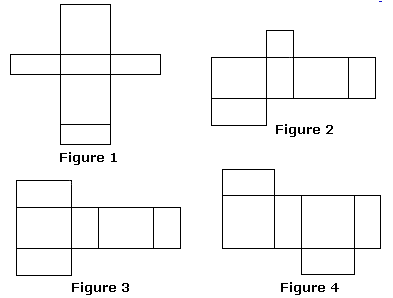
256: Nets - Rectangular Prism
Which of these could be a net for a rectangular prism (a box)?
If it cannot be folded into a box, which "face" would need to change and in what way?
If it cannot be folded into a box, which "face" would need to change and in what way?
Friday, September 19, 2014
255: Oscar Winners
Thursday, September 18, 2014
254: Football Puzzle
From Sam Loyd's Puzzle Encyclopedia:
We lived way back in the country and used to order our ball by mail, according to sizes advertised in a sporting house catalog, which advised patrons to "give the exact number of inches required," and that is where the problem comes in. We were told to give the size in inches, but we did not know whether it meant the number of square inches of rubber on the surface or the number of cubic inches of wind contained within the ball so we combined the two principles and ordered a ball which should contain just as many cubic inches of wind as it had superficial inches of surface!
How many of our puzzlists can guess the diameter of the ball which was ordered?
Wednesday, September 17, 2014
253: Half of the blocks have paint
I liked this puzzle, so I included it.
A rectangular wooden block (not necessarily a cube) is painted on the outside and then divided into one‐unit cubes. It turns out that exactly half of the cubes have paint on them. What were the dimensions of the block before it was painted?
(many answers)
So, where do we start?
What information is really being supplied here?
source.
Tuesday, September 16, 2014
252: Circle and Quarter-circles
What do you notice about the blue figure and the yellow one?
What could we do to find perimeter?
How about area?
Monday, September 15, 2014
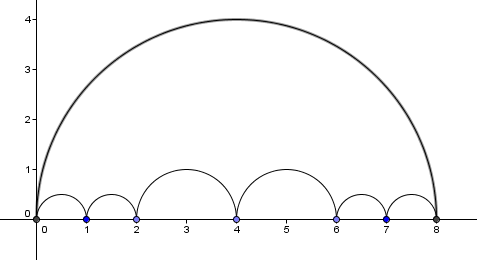
251: Semicircles 1
Let's talk about perimeter. What do you notice about the perimeter of the big semicircle alone and all of the smaller ones together?
What will happen if we changed this so that all the small semicircles were really, really, really small. Wouldn't that essentially be a straight line?
Sunday, September 14, 2014
250: The Shadow Knows
The man is walking down the sidewalk in the evening, at a constant speed. As he walks away from the streetlight, he casts a shadow in front of him.
If a second man were to try and keep up with the very front tip of his shadow, would he be walking at a constant speed, accelerating or decelerating, or what?
How do you know your answer is correct?
Saturday, September 13, 2014
249: Create some data
Can you create a set of data (more than 12 numbers, please) with a mean of 17 and a median of -17 and a mode of 0?
Friday, September 12, 2014
248: Raising one out of two.
Can you create a data set of more than 5 numbers so that when you add one additional number to the set, you can raise the median but not the mean?
Thursday, September 11, 2014
247: SAT Number theory
This is an actual SAT question, from later in a section so it is one that a lot of test-takers got wrong because it was a hard question, was worded strangely, had too many undefined letters, or was near the end of a section and the test-takers simply ran out of time.
What are some of the difficulties you think most students would have with it? What are some things we could do to rewrite the question so it's more clear?
Wednesday, September 10, 2014
246: Square and Circle
Two opposite vertices of a square lie on a circle. Sure as sunrises, someone is going to ask about area.
What information do we need?
What would be the easiest scenario?
Is there more than one easy scenario?
source.
Tuesday, September 9, 2014
245: Multiplication
What are some different ways we might find the greater product here?
Can you do this algebraically?
Graphically?
35 * 29 OR 39 * 25
Can you do this algebraically?
Graphically?
source: Fawn Nguyen @fawnpnguyen
Monday, September 8, 2014
Sunday, September 7, 2014
243: Powers and Squares
The process seems to be the interesting thing here. How would you begin to work on this?
source:
In how many ways can you write 2n as a difference of two squares?
source:
In how many ways can you write 2^n as a difference of two squares?
— James Tanton (@jamestanton)
Saturday, September 6, 2014
242: Trapezoid Puzzle
Friday, September 5, 2014
241: Mode not Median
Given the same numbers as we've been working with for a couple of days, along with an extra number X:
What values can X take on so that it is the mode but not the median?
X, 12783, 12784, 12785, 12790, 12792, 12795, 12799, 12801
What values can X take on so that it is the mode but not the median?
Thursday, September 4, 2014
240: Median not Average
Given the same numbers as we've been working with for a couple of days, along with an extra number X:
What values can X take on so that it is the median but not the average?
X, 12783, 12784, 12785, 12790, 12792, 12795, 12799, 12801
What values can X take on so that it is the median but not the average?
Wednesday, September 3, 2014
239: Outliers
Given the same numbers as we've been working with for a couple of days, along with an extra number X:
How small (or large) do you feel that value of x should be to be considered an outlier?
and of course, Ben Shabad, full-time graduate student and part-time cartoon-drawing person.
X, 12783, 12784, 12785, 12795, 12792, 12790, 12799, 12801
How small (or large) do you feel that value of x should be to be considered an outlier?
and of course, Ben Shabad, full-time graduate student and part-time cartoon-drawing person.
Tuesday, September 2, 2014
238: Skew
Given the same numbers as yesterday:
What characteristics can we look at to tell whether this data is skewed?
12783, 12784, 12785, 12790, 12792, 12795, 12799, 12811
What characteristics can we look at to tell whether this data is skewed?
Monday, September 1, 2014
237: Average
Given the numbers:
There are a lot of tricks and shortcuts, and of course, the pencil and paper add-em-up method of finding the average of a set of numbers.
What's your best way to get the average of those eight numbers?
12783, 12784, 12785, 12795, 12792, 12790, 12799, 12801
There are a lot of tricks and shortcuts, and of course, the pencil and paper add-em-up method of finding the average of a set of numbers.
What's your best way to get the average of those eight numbers?
Subscribe to:
Posts (Atom)