417: What can we do with this?

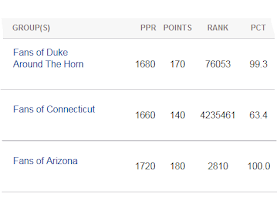
What can we do with this? There doesn't seem to be enough information.

416: What's wrong here?

What's the easiest way to fix this?

415: Parallels and Variables

Raw, pure math. Ummmmmm, tasty.

But can you make the question harder by rearranging the variables?

source:

Latest gems post - 5 maths teaching ideas http://t.co/tsIzPMVWzb #mathschat #mathstlp pic.twitter.com/Q4oW2J9sVO
— Jo Morgan (@mathsjem) March 9, 2015

414: Special Right Triangles

#mathsTLP Really must share this... Pythagoras meets surds - what's so special about these triangles? Higher GCSE pic.twitter.com/0v8vB6dEW4
— James Pearce (@MathsPadJames) March 22, 2015

413: Red and Blue Rubik

Suppose that a white Rubik's Cube is painted blue on top and bottom and painted red on the four lateral sides. The cube is then separated into its 27 smaller cubes. 

How many unit cubes have at least one red face and one blue face?

412: House Numbers

The houses on River Road are numbered consecutively from 10 to 132. Each house number is made with brass digits.

#105 would take 3 digits, for example.


1. How many brass digits are needed to form all the house numbers?

2. The numbers can be purchased for 2.29 each or $20.95 per dozen (of the same digit). What is the cheapest combination of numbers that you can arrange?

411: Say it out loud

If you can ...

410: Buying a cheap sweater to make a political point.

"The Wisconsin Republican's remarks, which received a standing ovation, started with the Badger State governor touting his middle class credentials. Before the speech, he had stopped by Kohl's Department Store and used Kohl's coupons to buy his sweater from the 70 percent off rack for one dollar.

Walker said he considered's Kohl's successful low-price strategy a model for reforming the tax code so that more people pay taxes, but the tax rate is much lower."

What the easiest way to find out the original cost of that sweater?

source.

From another site: "If you’ve ever shopped at Kohl’s, you know that it’s the store that generally always has a sale. Take a clearance item, apply a 15 percent off coupon with some Kohl’s Cash, and on the surface, Walker’s claim isn’t totally outrageous."

409: Pizza

That's an 18" diameter pizza plate.
It's the same area as that slice.
What's the girl's name?

Oh, you think you have a better question? Well, do you?

408: Balls

source.

407: The More Likely Sequence

Skimming the MTBoS Finds Interesting Things video from the Global Math department.

Which will be more likely to occur first

in a string of coin tosses, HTH or HTT?

This is the kind of question that becomes difficult because of assumptions made by the listener, assumptions that change the problem subtly and thus change the resulting expected probability. The listener/reader here naturally changes this question to "Which group of three is more likely?" That's not what he asked.
 
We should refer back to the Monty Hall question.
Source: Bob Lochel, Obvious Debate. from TEDTalk by Peter Donelly.

406: Bracketology

Here are my three brackets:

Which of these is most useful in determining how many people are playing?

How jealous are you right now?

405: Triangles

How much of the description is necessary in order to find the solution?

"an equilateral triangle and
three isosceles triangles
together make a rhombus

what must the angles in the rhombus be?"


Do we really need to know that it's a rhombus? Could we just be told it's a parallelogram?







source.

404: Best Argument Ever

[404: argument not found]

403: An Exponent Question

Considering the tweet below, which mental path do you think is easiest for beginning students?  (Analytical, numerical, graphical, algebraic?)

Would you give a different hint to beginning students than to advanced students?

#mathchat #SATPrep Will the average of 2^48 & 2^50 be <,>, or = 2^49?
Hint: Think graphically!
Now show the actual avg is 1.25×2^49.
— David Marain (@dmarain) March 18, 2015

402: Plugging in to Solve the SAT

This is from the end of a section of an SAT test, and is therefore a bitch to solve. At least, the results from the test seem to indicate so.  On a 5-choice multiple choice question, only 8% of respondents got this one right ... if they had covered their eyes, refused to read the question, and randomly guessed, they would have more than doubled their chances of getting it right. We can do better than that!

What numbers should I plug into the equations to test for correctness?

25. A watch loses x minutes every y hours. At this rate, how many hours will the watch lose in 1 week?

1. $7xy$
2. $\dfrac{7x}{y}$
3. $\dfrac{x}{7y}$
4. $\dfrac{14y}{5x}$
5. $\dfrac{14x}{5y}$

401: Which Question is Harder?

As we all know, the questions in an SAT test get harder as you get to the end of a section. I warn my students repeatedly that, at the end of a section,

"If you can't see what all those people thought was the obvious answer and clearly see why that obvious answer is wrong, then you are one of those who will jump to the wrong conclusion ... and you'll get it wrong, too."

 You see, the question at the end aren't really difficult usually. They can be badly worded but they're rarely HARD. They are usually four-step problems that everyone else is so sure about, and the answer is so obvious that they get suckered in. These two were rated the same level of difficulty, and were answered correctly by about 3%-5% of the students.

Which one is harder?

25. A woman drives to work each day at an average speed of 40 miles per hour and returns along the same route at 30 miles per hour. If her total traveling time was 1 hour, what was the total number of miles in the trip?

1. 30 
2. $30\dfrac{1}{7}$ 
3. $34\dfrac{2}{7}$ 
4. 35
5. 40

24. A 25 foot ladder is placed against a vertical wall of a building with the bottom of the ladder standing on concrete 7 feet from the base of the building. If the top of the ladder slips down 4 feet, then the bottom of the ladder will slide out.

1. 4ft 
2. 5ft 
3. 6ft 
4. 7ft 
5. 8ft

And can you say why the obvious answer is wrong?

400: Factoring

This problem, from Robert Kaplinsky, asks for you to fill in the spaces.

Being the ornery sort, I wondered if there were other coefficients that we could choose for the cubic that might give multiple sets of answers?

399: 3D Tangent?

Can a line be tangent to a circle? Sure, if they're coplanar.

What if they're NOT co-planar?

@MathCurmudgeon but beware the art teacher. They tend to think three-dimensionally. @calcdave
— sterlace (@sterlace) March 12, 2015

398: Two Tangents

Given: 2 tangents, one external and one internal.
The question was raised as to whether the large circle could be tangent at the intersection point.
What do you think?

Edit:

The fun part, of course, is "Can you explain that to the English teacher?" (force them to be clear but not too technical) ...

Alternatively, if those are tangents, can the circle go through the intersection point, even if not tangentially?

397: Substitutions

Based on a couple of posts I made a while back, Don Steward made these:

396: Rare Words

Why is that?