297: Systems of a Sort 3

A hotel rents a double-occupancy room for $30 more than a single-occupancy room. One night, the hotel took in $3115 after renting 15 double-occupancy rooms and 26 single-occupancy rooms. 

Other than by calling the hotel and asking directly, what ways could we use to find the single- and double- occupancy costs?

296: Systems of a Sort 2

What method works best to find the area of the triangle created by these three lines?
Organized list (a la excel)
Substitution?
Linear Combination?
Plug and Pray?

295: Systems of a Sort 1

In the following scenario, is there enough information to determine the cost of a bagel? Explain.

On Monday, the office staff at your school paid $8.75 for 4 cups of coffee and 7 bagels. On Wednesday, they paid $19.50 for 8 cups of coffee and 14 bagels. 

294: Equilateral Triangles and a square.

Equilateral triangles tile the plane. Is it possible to select four intersection points that are the corners of a perfect square?
— James Tanton (@jamestanton) October 18, 2014

293: Tight Fit

Seems as though this UHAUL truck got stuck.

Straightforward question: What's the diameter of that culvert?

Argument: What would have been a better way to phrase that sign so this wouldn't happen?

Dimensions

• Inside dimensions: 14'6" x 7'8" x 7'2" (LxWxH)
• Mom's Attic: 2'7" x 7'8" x 2'6" (LxWxH)
• Deck height: 2' 10"
• Door opening: 7'3" x 6'5" (WxH)
• Loading ramp width: 2'2"

292: What's This?

What is this?
What can we do with it?

Source.

291: Proof Without Words 7

What might all these kids be proving?

Source: Ed Southall (@edsouthall)

290: Teenage Birth Rates

Given the graph above, what do you think of this statement below?

289: Food Drive Cranberry Sauce

Quick, how many cans in the pyramid?

Same number of cans, different arrangement.

Because it's Christmas ...

288: Orange Pile

Quick ... more limes or more oranges?

287: Fahrenheit to Celsius

We all know the conversion from °C to °F: multiply by 9/5 (or 1.8, if you can't handle those evil fractions) and then add 32.

The conversion from °F to °C is more complex: subtract 32 and then multiply by 5/9 (or 0.555555555).

That's cumbersome for mental math.

Here's a shortcut: subtract 30 and divide by 2 OR multiply by 2 and add 30.

• How good is that shortcut?
• Are there temperatures that it's okay for and other temperatures that the shortcut is too far off?
• Is this just another stupid shortcut? NixTheTricks ?

286: Sphereometer

How does this thing work to find curvature?

What kinds of information do you need to make the markings on that dial?

285: Three Angles Revisited

Two days ago, I posted Okay for a Fifth-Grader?

Five Triangles said, "We posed the question slightly differently, our diagram providing an important hint to bring it to a more manageable level for younger problem solvers."

What do you suppose the "important hint" was?

284: Analyzing Digits

When the integers from 1 to 30 are multiplied, determine how many consecutive digits starting from the ones (1s) position are zeros.

Why does this question not require a calculator?

Would this be a fair question for some standardized test?

source.

283: Ok for a Fifth-Grader?

Three squares of equal but unknown size.

Is this a fair question to ask a fifth-grader?


From a Numberphile video.

282: Number puzzle

"The sum of two positive integers is 216. The greatest common factor of the two numbers is 24. What are all the possible pairs of numbers?"

What approach seems the easiest here?
I can see using solution methods such as:

• algebra
• guess and check
• organized list
• visual representation

Which (or which other) method rings true for you?
Which of the two sentences eliminates the most numbers?

The sum of 2 pos int is 216 and their gcf is 24. Find all possibilities.
— David Marain (@dmarain) September 24, 2014

281: Fix this Graph, Growth Edition

Oh, the horrors! What's wrong with this graph?

 

Fix That Graph !

source.

280: Rectangular Nets of Maximum Size - Connected

One possible arrangement.

If you wish, you can consider this problem to be one of wrapping paper around a small gift.

Find the net for the rectangular prism with the largest volume that you can make from a standard piece of paper (8.5" x 11"). Use whatever net arrangement of sides you prefer, but it has to be one connected net. (No loose pieces).

Find the sizes of the six rectangular pieces that form the rectangular prism with the largest volume that can be made from a standard piece of paper (8.5" x 11").

279: Rectangular nets of Maximum Size - Separate Pieces

Using a single sheet of 8.5x11 paper ... cover a rectangular solid. You can cut the paper.

What arrangement of rectangles seems to work best to cover it with no waste?

Which set of rectangles covers the prism with the largest possible volume?


"Find the sizes of the six rectangular pieces that can be made from a standard piece of paper (8.5" x 11") that that will cover the rectangular prism with the largest volume."

278: Adding powers.

Take a moment to consider the rules and the methods that we use with powers and exponents.



2^x + 2^x + 2^x + 2^x = 2²⁰¹⁴

x = ?

What is the "Aha!" thought, the epiphany, in this problem?

#SATPREP #Patterns #Algebra 2^x + 2^x + 2^x + 2^x = 2^2014 x=? Answer? Solutions? Strategies?
— David Marain (@dmarain) September 20, 2014

277: Central Tendency Mistakes

Expand that image to see details. As you peruse the list of values, how far can you get before you reach an inconsistency? Can we figure out what date each of the five pennies showed?

If you knew this was from a college teacher-education professor, would this change your opinion of the work shown in the picture?

276: Primes' Product and Sum

The really difficult questions on the SAT (the ones at the end of each section) are often not really that difficult -- they just seem to be hard to answer because they're hard to read and understand because of the formal mathematical writing style and the complexity of the sentence. Often the best tactic is to plug in some numbers for the vague-sounding variables and make the problem more concrete.

"The positive number k is the product of four different positive prime numbers.
If the sum of these four prime numbers is a prime number greater than 20,
what is the least possible value for k?"

So what can we do with this one to make it simpler to understand the question?
Where would you start?

275: Subtracting a series.

If you're a junior or senior, you've seen versions of this problem before, perhaps on the SAT (the source of this problem). As I've said before, the SAT is designed in a way that calculators are not necessary and each question must be solvable in less than a minute. Often, the student is expected to change the form of the question: text to algebra, or algebra to visual (graphical); or rearrange the terms, or work backwards from the known. 

The sum of the positive odd integers less than 200 is subtracted
from the sum of the positive even integers less than or equal to 200.
What is the resulting difference?

As it stands, that question would take you far too long to find an answer for, so it must have a simplification somewhere.

What can we do to make this quicker to answer?
Or simpler to understand?

How can we change it?

274: Two towns are Far Apart.

Town A is 300 km from Town B and Town B is 200 km away from Town C.

• What is the closest A and C could be?
• How far apart could they be, if they were as far apart as possible?
• How many integer distances  between A&C are possible?

#SATPREP Town A is 300 km from B which is 200 km from C. How many integer distances between A&C are possible?
— David Marain (@dmarain)

273: Ranking performance

My ranking for March Madness ... as you can see, I didn't do very well.

What information can we glean from this?

272: Orthic Triangle

What do you notice about the "orthic triangle"?

Is its area related to the area of ABC?
Is it similar?
What other triangles could be made with other features of triangle ABC (medians, angle bisectors)?

source:

Next time you teach types of triangle, throw in the orthic triangle to make it a bit less BORING. pic.twitter.com/KlSu9qzf4B
— Ed Southall (@edsouthall)

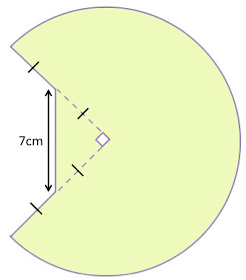
271: Oddball Area, #5

Assuming the vertex of the angle is at the center.
Should we add pieces together to make this or subtract pieces?
What are the relevant dimensions?

source.

270: Intersecting Planes

1a. Look at the examples above. Is that the whole list of possibilities or are there other ways to answer the question, "How can three planes intersect?"
1b. What are the intersections in each case?

2. How can four planes intersect?

269: Probability Sums

5 distinct numbers are chosen at random from {1,2,3,4,5,6,7,8,9}.

p(k) = probability their sum = k.

What are some of the ways you can find this in general?
What sum is/are the least likely?
Which sum is/are most likely?

p(15)=?

p(35)=?

source:

5 distinct numbers are chosen at random from {1,2,3,4,5,6,7,8,9}. p(k) = probability their sum = k. p(15)=?,..., p(35)=?
— Republic of Math (@republicofmath)

and

Five distinct nmbrs chosen at random from {1,2,3,...,9} and added together. What is the most likely sum?
— James Tanton (@jamestanton)

268: Obscure Geometry

from: @ddmeyer

267: Date puzzle

The day before yesterday Edward was 17.  Next year he will be 20.  How can that be the case?